Contoh Soal Statistika Dan Pembahasannya
Contoh Soal Statistika Dan Pembahasannya Rating: 4,3/5 4376 votes
Choose thecorrect answer!
1. Ming and Andrew made a cake and cutit into 8 equal pieces. They gave 3 pieces to Susan. What fraction of the cakeis left?
B. 5/8
D. 1/8
Soal Ulangan Harian Statistika Matematika Kelas 8 Kurikulum 2013 dan Pembahasannya ini merupakan contoh soal terbaru yang akan saya bagikan bagi Bapak/Ibu yang mengampu mata pelajaran Matematika Kelas 8 SMP/MTs yang telah menerapkan Kurikulum 2013. Itulah contoh soal dan pembahasan tentang distribusi binomial. Yang paling penting dipahami adalah bagaimana menentukan: n, x, p dan q. Jika sudah bisa mengidentifikasi hal tersebut maka untuk menghitung sangatlah mudah dengan menggunakan rumus yang telah ada.
Subtract the loss from your previous inventory balance and report the new amount on your balance sheet. Continuing the example, assume the expired food was. Free product sheet template.
2. Steve checked out a book and avideo from the local library. They were three days overdue when he returnedthem. The fine was 15 cents for each day the book was overdue, and 25 cents foreach day the video was overdue. How much did Steve owe?
B.$0.45
D.$1.20
3. Inart class, Raúl was given the shapes shown below.
Raúlused some of the shapes to make a design that had 2 lines of symmetry. Which ofthe following could be his design?
4. Tituswent to the pet store to buy the following items for his dog.
Whichof the following is the least amount of money needed to pay for all ofhis items?
·5 grey balls,
·4 striped balls.
If shetakes a ball out of the bag without looking, what are her chances of getting awhite ball?
B. 3chances out of 9
D. 9chances out of 12
6. Whichof the following is equal to 104 X 50?
B.(100 X 5) + (4 X 50)
D.(100 X 50) + (40 X 50)
7. Jamal started playing a video gameat 4:30 P.M. When the game was over, he looked at his watch which showed thistime.
Howlong did the game last?
B. 1hour, 15 minutes
D.45 minutes
8.Martadrew the figure shown below.
InMarta’s drawing, which two line segments appear to be parallel?
B.II and III
D.IV and V
9.Ata class party, 3 pizzas were ordered for the children. Each pizza was dividedinto 8 equal slices.
Eachchild ate 2 slices, and there was a quarter of one pizza left. How manychildren were at the party?
B.12
D.22
10.Admissionto the Basketball Hall of Fame in Springfield is $5.00 per student. A group ofstudents bought admission tickets. One student spent an extra $9.00 for aposter. The total amount they spent was $34.00. How many students were in thegroup?
B. 5
D. 7
11.Harry has 6 markers, and Rico has 10 markers.Which of the following actions would result in Harry and Rico having the samenumber of markers?
B.Harry gives 4 of his markers to Rico.
D.Rico gives 4 of his markers to Harry.
12. Micah left for school with 4 boxesof pencils. Each box had 6 pencils. At school, he gave away 4 pencils from onebox. Which number sentence below can be used to find the total number ofpencils that were left?
13. Which point is incorrectly labeled on the number line shown below?
14. Jesse and Fred shared a pizza.Jesse ate 1/8 of the pizza, and Fred ate 1/2 of the pizza. Which picture showshow much pizza was left?
15. A newsculpture was built in a city park. The diagrams below show the top view andthe side view of the sculpture.
Which of thefollowing pictures best shows the shape of the sculpture?
16. Tynan used small squares to makeeach figure shown in the arithmetic pattern below.
Ifthe pattern continues, how many small squares will be in Figure 10?
B.22
D.26
17. Louise was reciting the 26 lettersof the alphabet in groups of 3: 'ABC, DEF, GHI, . . . ' Before shecould finish, her friend Heather said, 'There will be 2 letters leftover.'
Whichof the following suggests that Heather is correct?
B. 6divided by 3 equals 2.
D.26 divided by 4 leaves a remainder of 2.
18. Ryan, Jodi, Tess, and Jeremy had acheckers tournament. The chart below shows the results.
Whichplayer won exactly 1/2 of the games that he or she played?
B.Jodi
D.Jeremy
19. Claire has 3 bags of marbles with8 marbles in each bag. Leo has 8 bags of marbles with 3 marbles in each bag.Which number sentence shows that Claire and Leo have the SAME number ofmarbles?
B. 8- 3 = 3 - 8
D. 8- 3 = 5
20. A pattern was used to determinethe number of black tiles and the number of white tiles in each figure below.
Ifthe pattern continues, how many black tiles will there be in Figure 5?
B. 4
D. 7
21. The line plot below shows how students scored on last week’s vocabularytest.
Howmany students scored 95 or higher on the test?
B. 7students
D.16 students
22. Which word problem below could be represented by the number sentence 5X 3 = 15?
A. Lynda had 5 notebooks. She bought 3 morenotebooks. How many notebooks did she have?
B. Lynda bought 5 packages of notebooks with 3notebooks in each package. How many notebooks did she buy?
C. Lynda had 5 notebooks. She gave away 3 of them.How many notebooks did she have left?
D. Lynda had 5 packages of notebooks. She put thenotebooks in 3 stacks. How many notebooks were in each stack?
23. Which of the following does not represent 0.4?
24. Minh opened a bottle containing 1liter of juice. If she shared the juice equally with her sister Anne, how manymilliliters (mL) of juice will each get? (1 liter = 1000 mL)
A.20 milliliters
C.200 milliliters
25. Dwayne used a rule to make the list of numbers shown.
Ifhe uses the same rule to continue the list, which number should he write next?
B.22
D.26
26. Amelia has 47 strawberries to putin 5 baskets. She wants to put the same number of strawberries in each basket.If she evenly divides the strawberries among the 5 baskets, how manystrawberries will be left over?
B. 2
D. 3
27. For a school project, Quentin hadto make a grid map of his back yard. His map looked like this:
Whichordered pair gives the location of the doghouse?
B.(5, 1)
D.(1, 5)
28. Which ofthese numbers is evenly divisible by 3?
B. 1,687,093
D. 2,687,096
29. Use the map below to answer question 29.
Which two streets onthe map above appear to be parallel?
B. Broadway andPlymouth
D. Adams and Revere
30. The stem-and-leaf plot below shows how a classof sixth-graders scored on a math test.
A score of 63 orhigher is passing. How many sixth-graders passed this math test?
B. 13
D. 17
31.Sara hiredher brother James to help her sell lemonade. Sara agreed to pay James $1.00,plus $0.10 for each glass of lemonade that he sold. Sara paid James $3.60. Howmany glasses of lemonade did James sell?
B. 36
D. 56
32. Teresa iscovering the floor of her kitchen with tiles. Each square tile covers 4 squarefeet. If her kitchen floor is a rectangle measuring 16 feet by 10 feet, howmany tiles will she need?
B. 26
D. 40
33. Use the spinner below to answer question 33.
Ramón is going to spinthe arrow on the spinner twice and add the results. What is the most likely sumof the two spins?
B. 8
D. 12
34. Earth’satmosphere is 78.08% nitrogen and 20.95% oxygen. What percent of Earth’satmosphere is made up of gases other than nitrogen and oxygen?
B. 0.097
D. 97
35. Each of the 6 small squares in the figure belowmeasures 1 inch on each side.
Which of the followingis closest to the area of the shaded portion of the figure?
B. 3 square inches
D. 5 square inches
36. The linebelow shows the locations of three towns on a highway. The distance fromWestfield to Springfield is 10 miles, and the distance from Westfield to Palmeris 25 miles. What is the distance, in miles, from Springfield to Palmer?
B. 20
D. 35
37. An architect measured the three angles markedin the diagram below.
What was the sum ofthe measures of the three angles?
B. 210 degrees
D. 360 degrees
38. Mariacharges $5.00 to mow a lawn, plus $6.00 per hour. Maria uses the equation C =5 + 6h to determine C, the amount of money she charges for mowinglawns. If h represents the number of hours it takes to mow a lawn, howmuch money will Maria charge if she mows a lawn for 3 hours?
B. $14.00
D. $23.00
39. The graph below shows the speed of a droppedobject over time.
Based on the graph,what will be the approximate speed of the dropped object after 5 seconds?
Contoh Soal Dan Pembahasan Statistika
B. 25 meters persecond
D. 75 meters persecond
40.The table shows the temperature on four wintermornings in the Berkshire Mountains.
Which day had thewarmest morning?
B. Friday
D. Sunday
41. Lily designed the kite below for an experiment.
Which of the followingcorrectly describes the shape of Lily’s kite?
B. rectangle
D. quadrilateral
42.Use the table below to answer question 42.
According to thepattern shown, what is the value of y when x is 12?
B. 60
D. 100
43. Hansurveyed 15 of her classmates to find their shoe sizes. She displayed the datain the line plot below.
What is the medianshoe size?
B. 6
D. 10
44. Doloresbought a package of corn seeds. She wanted to use all the seeds in the packageto plant two or more rows of corn with the same number of seeds in each row,but she found that this was not possible. Which of the following couldhave been the number of seeds in the package?
B. 33
D. 37
45. Sherrie is sewing a costume for a party. She isusing the pattern shown below.
Which of the followingpieces of cloth is congruent to the pattern?
46. Cai boughtpopcorn for herself and 2 friends, plus a drink only for herself. The popcorncost $2 for each person, and the total cost for Cai’s purchase was $7.50. If dis the cost of a drink, which equation below could be used to determine thecost of Cai’s drink?
B. 2 + 2d =$7.50
D. 3(2) + 3d =$7.50
48. Sylvia andTomás are playing a game of chess. Each player began the game with 16 pieces.Now Sylvia has 1/4 of her pieces remaining on the board and Tomás has 1/8 ofhis pieces remaining on the board. How many total pieces remain on the board?
B. 6
D. 12
49. Which number line below best representsthe addition problem
50.The chart below lists the times it took fourstudents to run the 50-yard dash.
Which shows thestudents in order from fastest to slowest?
B. Carlos, John, Sam,Pete
D. Carlos, Sam, John,Pete
1 | 11 | 21 | 31 | 41 |
2 | 12 | 22 | 32 | 42 |
3 | 13 | 23 | 33 | 43 |
4 | 14 | 24 | 34 | 44 |
5 | 15 | 25 | 35 | 45 |
6 | 16 | 26 | 36 | 46 |
7 | 17 | 27 | 37 | 47 |
8 | 18 | 28 | 38 | 48 |
9 | 19 | 29 | 39 | 49 |
10 | 20 | 30 | 40 | 50 |
Soal Dan Pembahasan Statistik
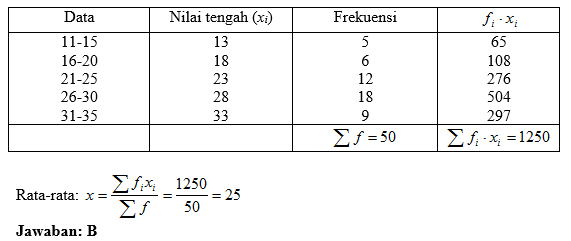
Selain dalam bentuk diagram, penyajian data juga dengan menggunakan tabel distribusi frekuensi. Berikut ini akan dipelajari lebih jelas mengenai tabel distribusi frekuensi tersebut.
1. Distribusi Frekuensi Tunggal
Data tunggal seringkali dinyatakan dalam bentuk daftar bilangan, namun kadangkala dinyatakan dalam bentuk tabel distribusi frekuensi. Tabel distribusi frekuensi tunggal merupakan cara untuk menyusun data yang relatif sedikit. Perhatikan contoh data berikut.
5, 4, 6, 7, 8, 8, 6, 4, 8, 6, 4, 6, 6, 7, 5, 5, 3, 4, 6, 6
8, 7, 8, 7, 5, 4, 9, 10, 5, 6, 7, 6, 4, 5, 7, 7, 4, 8, 7, 6
2. Distribusi Frekuensi Bergolong
Tabel distribusi frekuensi bergolong biasa digunakan untuk menyusun data yang memiliki kuantitas yang besar dengan mengelompokkan ke dalam interval-interval kelas yang sama panjang. Perhatikan contoh data hasil nilai pengerjaan tugas Matematika dari 40 siswa kelas XI berikut ini.
66 75 74 72 79 78 75 75 79 71
75 76 74 73 71 72 74 74 71 70
74 77 73 73 70 74 72 72 80 70
73 67 72 72 75 74 74 68 69 80
Apabila data di atas dibuat dengan menggunakan tabel distribusi frekuensi tunggal, maka penyelesaiannya akan panjang sekali. Oleh karena itu dibuat tabel distribusi frekuensi bergolong dengan langkah-langkah sebagai berikut.
a. Mengelompokkan ke dalam interval-interval kelas yang sama panjang, misalnya 65 – 67, 68 – 70, … , 80 – 82. Data 66 masuk dalam kelompok 65 – 67.
b. Membuat turus (tally), untuk menentukan sebuah nilai termasuk ke dalam kelas yang mana.
c. Menghitung banyaknya turus pada setiap kelas, kemudian menuliskan banyaknya turus pada setiap kelas sebagai frekuensi data kelas tersebut. Tulis dalam kolom frekuensi.
d. Ketiga langkah di atas direpresentasikan pada tabel berikut ini.
Istilah-istilah yang banyak digunakan dalam pembahasan distribusi frekuensi bergolong atau distribusi frekuensi berkelompok antara lain sebagai berikut.
a. Interval Kelas
Tiap-tiap kelompok disebut interval kelas atau sering disebut interval atau kelas saja. Dalam contoh sebelumnya memuat enam interval ini.
65 – 67 → Interval kelas pertama
68 – 70 → Interval kelas kedua
71 – 73 → Interval kelas ketiga
74 – 76 → Interval kelas keempat
77 – 79 → Interval kelas kelima
80 – 82 → Interval kelas keenam
b. Batas Kelas
Berdasarkan tabel distribusi frekuensi di atas, angka 65, 68, 71, 74, 77, dan 80 merupakan batas bawah dari tiap-tiap kelas, sedangkan angka 67, 70, 73, 76, 79, dan 82 merupakan batas atas dari tiap-tiap kelas.
c. Tepi Kelas (Batas Nyata Kelas)
Untuk mencari tepi kelas dapat dipakai rumus berikut ini.
Tepi bawah = batas bawah – 0,5
Tepi atas = batas atas + 0,5
Dari tabel di atas maka tepi bawah kelas pertama 64,5 dan tepi atasnya 67,5, tepi bawah kelas kedua 67,5 dan tepi atasnya 70,5 dan seterusnya.
d. Lebar kelas
Untuk mencari lebar kelas dapat dipakai rumus:
Lebar kelas = tepi atas – tepi bawah
Jadi, lebar kelas dari tabel diatas adalah 67,5 – 64,5 = 3.
e. Titik Tengah
3. Distribusi Frekuensi Kumulatif
Daftar distribusi kumulatif ada dua macam, yaitu sebagai berikut.
a. Daftar distribusi kumulatif kurang dari (menggunakan tepi atas).
b. Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah).
Untuk lebih jelasnya, perhatikan contoh data berikut ini.
4. Histogram
Dari suatu data yang diperoleh dapat disusun dalam tabel distribusi frekuensi dan disajikan dalam bentuk diagram yang disebut histogram. Jika pada diagram batang, gambar batang-batangnya terpisah maka pada histogram gambar batang-batangnya berimpit. Histogram dapat disajikan dari distribusi frekuensi tunggal maupun distribusi frekuensi bergolong. Untuk lebih jelasnya, perhatikan contoh berikut ini. Data banyaknya siswa kelas XI IPA yang tidak masuk sekolah dalam 8 hari berurutan sebagai berikut.
5. Poligon Frekuensi
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya
dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas dapat dibuat poligon frekuensinya seperti gambar berikut ini.
6. Poligon Frekuensi Kumulatif
Dari distribusi frekuensi kumulatif dapat dibuat grafik garis yang disebut poligon frekuensi kumulatif. Jika poligon frekuensi kumulatif dihaluskan, diperoleh kurva yang disebut kurva ogive. Untuk lebih jelasnya, perhatikan contoh soal berikut ini.
b. Ogive naik dan ogive turun
Daftar frekuensi kumulatif kurang dari dan lebih dari dapat disajikan dalam bidang Cartesius. Tepi atas (67,5; 70,5; …; 82,5) atau tepi bawah (64,5; 67,5; …; 79,5) diletakkan pada sumbu X sedangkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari diletakkan pada sumbu Y. Apabila titik-titik yang diperlukan dihubungkan, maka terbentuk kurva yang disebut ogive. Ada dua macam ogive, yaitu ogive naik dan ogive turun. Ogive naik apabila grafik disusun berdasarkan distribusi frekuensi kumulatif kurang dari. Sedangkan ogive turun apabila berdasarkan distribusi frekuensi kumulatif lebih dari. Ogive naik dan ogive turun data di atas adalah sebagai berikut.
1. Distribusi Frekuensi Tunggal
Data tunggal seringkali dinyatakan dalam bentuk daftar bilangan, namun kadangkala dinyatakan dalam bentuk tabel distribusi frekuensi. Tabel distribusi frekuensi tunggal merupakan cara untuk menyusun data yang relatif sedikit. Perhatikan contoh data berikut.
5, 4, 6, 7, 8, 8, 6, 4, 8, 6, 4, 6, 6, 7, 5, 5, 3, 4, 6, 6
8, 7, 8, 7, 5, 4, 9, 10, 5, 6, 7, 6, 4, 5, 7, 7, 4, 8, 7, 6
2. Distribusi Frekuensi Bergolong
Tabel distribusi frekuensi bergolong biasa digunakan untuk menyusun data yang memiliki kuantitas yang besar dengan mengelompokkan ke dalam interval-interval kelas yang sama panjang. Perhatikan contoh data hasil nilai pengerjaan tugas Matematika dari 40 siswa kelas XI berikut ini.
66 75 74 72 79 78 75 75 79 71
75 76 74 73 71 72 74 74 71 70
74 77 73 73 70 74 72 72 80 70
73 67 72 72 75 74 74 68 69 80
Apabila data di atas dibuat dengan menggunakan tabel distribusi frekuensi tunggal, maka penyelesaiannya akan panjang sekali. Oleh karena itu dibuat tabel distribusi frekuensi bergolong dengan langkah-langkah sebagai berikut.
a. Mengelompokkan ke dalam interval-interval kelas yang sama panjang, misalnya 65 – 67, 68 – 70, … , 80 – 82. Data 66 masuk dalam kelompok 65 – 67.
b. Membuat turus (tally), untuk menentukan sebuah nilai termasuk ke dalam kelas yang mana.
c. Menghitung banyaknya turus pada setiap kelas, kemudian menuliskan banyaknya turus pada setiap kelas sebagai frekuensi data kelas tersebut. Tulis dalam kolom frekuensi.
d. Ketiga langkah di atas direpresentasikan pada tabel berikut ini.
Istilah-istilah yang banyak digunakan dalam pembahasan distribusi frekuensi bergolong atau distribusi frekuensi berkelompok antara lain sebagai berikut.
a. Interval Kelas
Tiap-tiap kelompok disebut interval kelas atau sering disebut interval atau kelas saja. Dalam contoh sebelumnya memuat enam interval ini.
65 – 67 → Interval kelas pertama
68 – 70 → Interval kelas kedua
71 – 73 → Interval kelas ketiga
74 – 76 → Interval kelas keempat
77 – 79 → Interval kelas kelima
80 – 82 → Interval kelas keenam
b. Batas Kelas
Berdasarkan tabel distribusi frekuensi di atas, angka 65, 68, 71, 74, 77, dan 80 merupakan batas bawah dari tiap-tiap kelas, sedangkan angka 67, 70, 73, 76, 79, dan 82 merupakan batas atas dari tiap-tiap kelas.
c. Tepi Kelas (Batas Nyata Kelas)
Untuk mencari tepi kelas dapat dipakai rumus berikut ini.
Tepi bawah = batas bawah – 0,5
Tepi atas = batas atas + 0,5
Dari tabel di atas maka tepi bawah kelas pertama 64,5 dan tepi atasnya 67,5, tepi bawah kelas kedua 67,5 dan tepi atasnya 70,5 dan seterusnya.
d. Lebar kelas
Untuk mencari lebar kelas dapat dipakai rumus:
Lebar kelas = tepi atas – tepi bawah
Jadi, lebar kelas dari tabel diatas adalah 67,5 – 64,5 = 3.
e. Titik Tengah
3. Distribusi Frekuensi Kumulatif
Daftar distribusi kumulatif ada dua macam, yaitu sebagai berikut.
a. Daftar distribusi kumulatif kurang dari (menggunakan tepi atas).
b. Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah).
Untuk lebih jelasnya, perhatikan contoh data berikut ini.
4. Histogram
Dari suatu data yang diperoleh dapat disusun dalam tabel distribusi frekuensi dan disajikan dalam bentuk diagram yang disebut histogram. Jika pada diagram batang, gambar batang-batangnya terpisah maka pada histogram gambar batang-batangnya berimpit. Histogram dapat disajikan dari distribusi frekuensi tunggal maupun distribusi frekuensi bergolong. Untuk lebih jelasnya, perhatikan contoh berikut ini. Data banyaknya siswa kelas XI IPA yang tidak masuk sekolah dalam 8 hari berurutan sebagai berikut.
5. Poligon Frekuensi
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya
dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas dapat dibuat poligon frekuensinya seperti gambar berikut ini.
6. Poligon Frekuensi Kumulatif
Dari distribusi frekuensi kumulatif dapat dibuat grafik garis yang disebut poligon frekuensi kumulatif. Jika poligon frekuensi kumulatif dihaluskan, diperoleh kurva yang disebut kurva ogive. Untuk lebih jelasnya, perhatikan contoh soal berikut ini.
b. Ogive naik dan ogive turun
Daftar frekuensi kumulatif kurang dari dan lebih dari dapat disajikan dalam bidang Cartesius. Tepi atas (67,5; 70,5; …; 82,5) atau tepi bawah (64,5; 67,5; …; 79,5) diletakkan pada sumbu X sedangkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari diletakkan pada sumbu Y. Apabila titik-titik yang diperlukan dihubungkan, maka terbentuk kurva yang disebut ogive. Ada dua macam ogive, yaitu ogive naik dan ogive turun. Ogive naik apabila grafik disusun berdasarkan distribusi frekuensi kumulatif kurang dari. Sedangkan ogive turun apabila berdasarkan distribusi frekuensi kumulatif lebih dari. Ogive naik dan ogive turun data di atas adalah sebagai berikut.